F the Rectangle Below is Continuously Rotated About Side W Which Solid Figure is Formed
| In this section, we will be rotating (spinning) a two-dimensional figure about a line to produce a three-dimensional shape, called a solid of revolution.
An example of a rotation about a line is the concept of a revolving door. The panel of one section of the glass door is "pushed" about a center pole, creating an outer cylindrical path around the pole. While the revolving door does not create a "solid", it does illustrate the process of revolution. If the door filled the entire space as it revolved, a cylindrical solid would be formed.
With the idea of revolution (rotation) in mind,
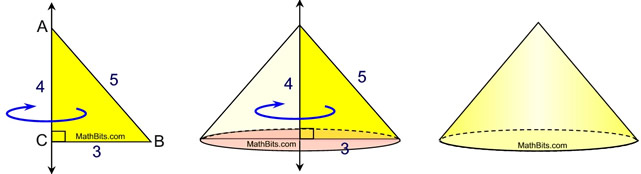
Note: If the 2-D figure (or a portion of the figure) is shaded, then that portion of the 3-D figure will be solid when the revolution occurs.
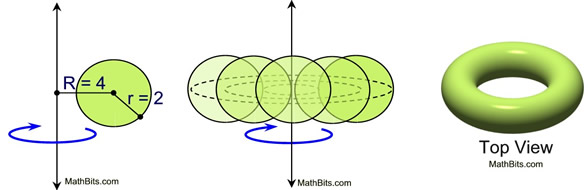
Note: If the 2-D figure is not tangent (touching) to the line of rotation (axes) , then the solid will be in the form of a "ring", with an open section between portions of the solid.
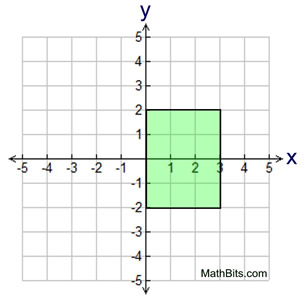
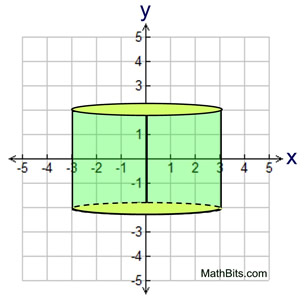
Note: The 2-D figure may appear on coordinate axes, from which you can obtain measurement information about the figure. Rotations will most likely be about the y-axis or the x-axis (but may be about any vertical or horizontal line.)
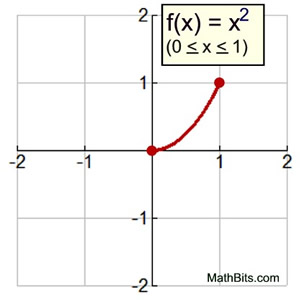
Note: It may be the case that a portion of a function (or functions) will represent the 2-D figure on coordinate axes to be revolved about an axis or a vertical or horizontal line.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation | ||||||||||||||||||||||||
Source: https://mathbitsnotebook.com/Geometry/3DShapes/3DRotations.html


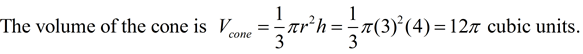
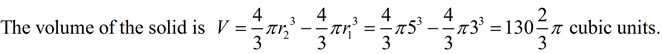
0 Response to "F the Rectangle Below is Continuously Rotated About Side W Which Solid Figure is Formed"
แสดงความคิดเห็น